In this article, we will consider a mathematical formula for the basics of cornering. Cornering, together with accelerating and braking, is one of the characteristic motions of a vehicle. According to Newton’s laws of motion, the motion of an object is expressed as a relational equation between force and acceleration. During cornering, acceleration occurs in the lateral direction of the vehicle. It is therefore the purpose of this article specifically to express the lateral acceleration in mathematical formulae. The key factors are the vehicle yaw rate and the body slip angle.
Table of Contents
The Focus of Vehicle Dynamics: The Act of Cornering
In the field of vehicle dynamics, the primary focus lies on the act of ‘cornering’ among the basic vehicle operations of accelerating, cornering, and braking.
This focus is due to the unique ability of vehicles to freely change direction based on the driver’s steering, distinguishing them from trains and other rail-bound systems.
The Starting Point: Uniform Circular Motion
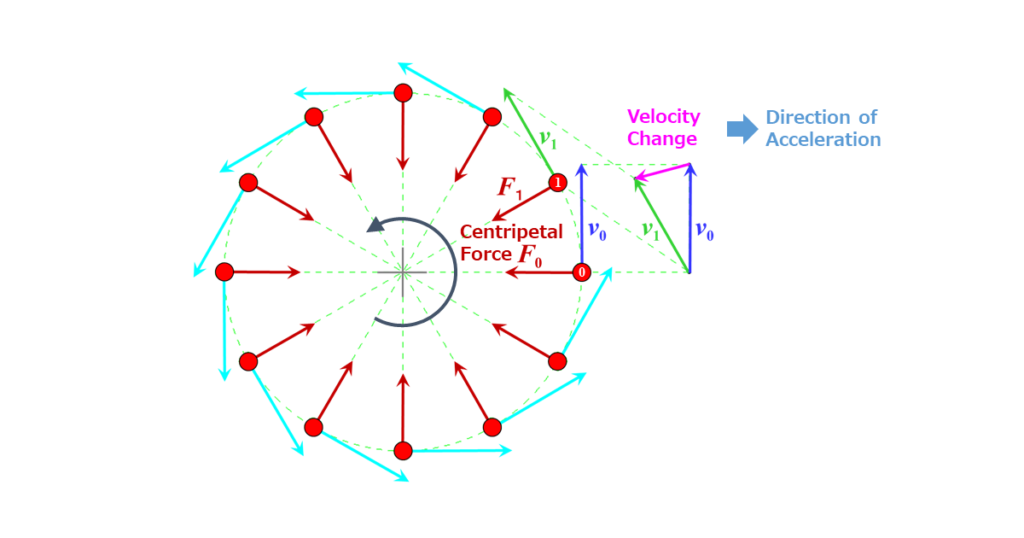
To understand vehicle dynamics, let’s first consider the motion of a point mass – an idealized object with mass but no size or shape.
Imagine a point mass moving at a constant speed in a counterclockwise circle.
Here’s what happens:
- Constant Speed, Variable Velocity: The speed stays unchanged, but the velocity, which is directional, is always changing, aligning with the circle’s tangent.
- Acceleration Arises: Since there is a velocity change, acceleration is occurring. The direction of the acceleration is equal to the direction of the velocity change. This means that the acceleration is directed toward the center of the circle.
- Centripetal Force: According to Newton’s laws, this acceleration must be caused by a force – the centripetal force, which, in vehicles, is provided by tire traction.
For more info, please see the following article.
Unraveling the Mystery of Lateral G-Forces in Race Cars
From Point Mass to Vehicle Cornering
When we scale up from a point mass to an actual vehicle, the complexity increases. A vehicle’s motion is not just about moving along a path but also involves its orientation. Thus, we consider:
- Lateral Movement of the Center of Gravity: This involves the sideways movement of the vehicle’s mass center.
- Yaw Motion of the Vehicle Body: This is the rotational motion around the vertical axis, crucial in determining the vehicle’s direction.
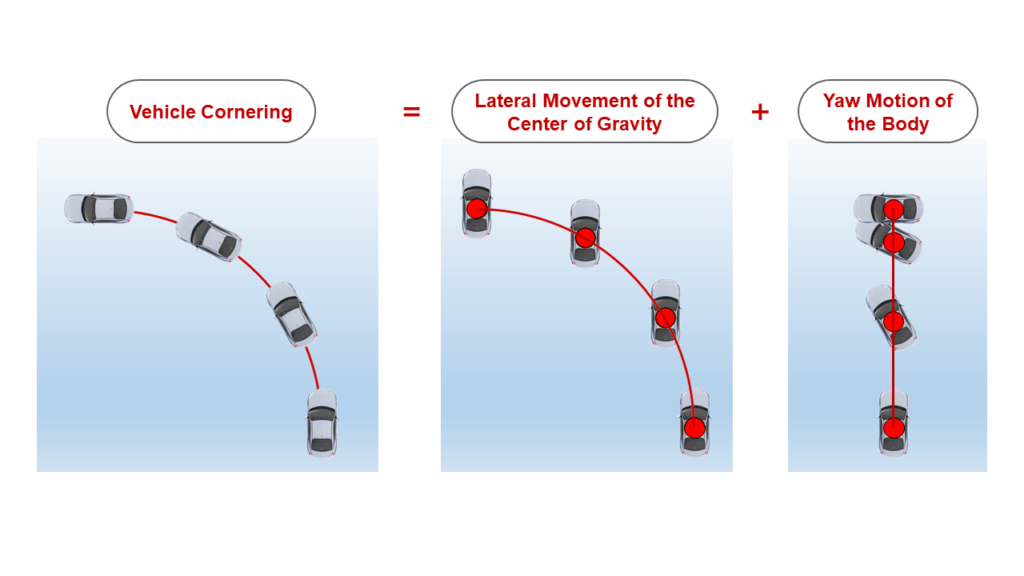
In vehicle dynamics, these two motions are intertwined. Notably, the vehicle’s orientation might not always correspond with the direction of motion, as vividly demonstrated in drifting maneuvers.
Defining the Coordinate System
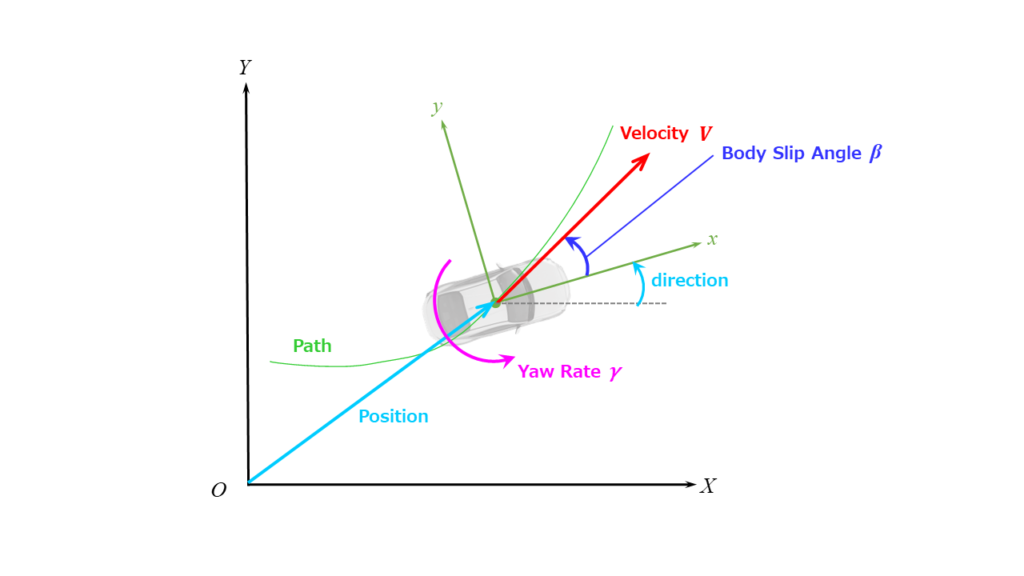
Vehicle motion is typically analyzed in a moving coordinate system fixed to the vehicle.
The origin is at the vehicle’s center of gravity, with the x-axis aligned with the vehicle’s longitudinal direction (forward being positive).
Neither the vehicle’s position nor its direction is crucial; instead, motion is considered in terms of velocity and angular velocity (yaw rate, denoted as \(\gamma\)).
The angle of velocity relative to the x-axis (counter-clockwise being positive) is called the body slip angle (denoted as \(\beta\)).
Lateral Acceleration: The Key Metric
Circular motion is caused by a force transverse to the direction of travel. According to Newton’s laws of motion, a lateral (y-axis) acceleration is produced at that time, so let us consider an equation to express this.
It is the sum of the following two components:
- The time derivative of \(V_y\) : $$\dot{V_y}$$
- The directional change of \(V_x\) due to the yaw rate: $$V_x\cdot\gamma$$
When discussing handling, the body slip angle \(\beta\) can be considered sufficiently small, so the following approximation holds:
$$V_y=V\sin\beta\approx V\beta$$ $$V_x=V\cos\beta\approx V$$
Thus, the lateral acceleration is described as:
$$a_y=\dot{V_y}+V_x\cdot\gamma\approx V\cdot\dot{\beta}+V\cdot\gamma=V(\dot{\beta}+\gamma)$$
This implies that:
Steady-State Cornering
Using the formula \(a_y=V(\dot{\beta}+\gamma)\), various vehicle motions can be expressed.
In steady-state cornering, the body slip angle stays constant. i.e.
$$\dot{\beta}=0$$
Therefore,
$$a_y=V\gamma$$
Conclusion for the Basics of Cornering
The exploration of vehicle dynamics, particularly the mathematical modeling of ‘turning,’ provides invaluable insights into the intricate dance between a vehicle and the laws of physics. It empowers engineers to push the boundaries of automotive design and safety. As we continue to advance in technology and understanding, the principles laid out in this field will undoubtedly lead to more innovative and efficient vehicles, altering our experience of mobility and transportation. In essence, the mathematics of vehicle movement is not just about numbers and equations; it’s about understanding the harmony between man, machine, and motion.




