In the racing world, the slightest difference can make the difference between winning and losing. By understanding vehicle dynamics, engineers can optimize vehicle behavior and improve performance.
One key concept in understanding the fundamentals of race car dynamics is acceleration. Acceleration is essential because it is related to Newton’s second law of motion.
Table of Contents
Understanding Newton’s Second Law of Motion
Newton’s second law of motion (or Newton’s equation of motion) can be represented by the equation:
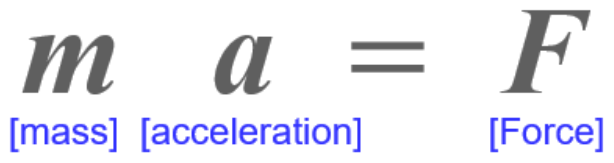
It means that when you apply a force to a car, the car accelerates in the same direction as the force. The acceleration (a) is proportional to the force (F) and inversely proportional to the car’s mass (m).
You may be more familiar with the form F=ma. Of course, this could also be correct. However, I use the form ma=F according to the concept of the law of causality.
The law of causality means that an equation not only equals the left and right sides but also expresses a causal relationship with the result on the left side and the cause on the right side.
In this case, the acceleration is the result, and the force is the cause, so the equation is written in this order.
In the case of a car, the forces are the driving force generated by the engine, the braking force generated by the brakes, the cornering force generated by the tires, and so on. When these forces act on the car, the car experiences acceleration.
So, what is acceleration?
Understanding Acceleration
Initially, when considering acceleration, we must take direction into account. For this discussion, let’s focus on acceleration in the direction the car is moving.
Acceleration is how quickly a car’s speed changes. If you draw a graph with time and speed, acceleration is shown by the slope of the line.
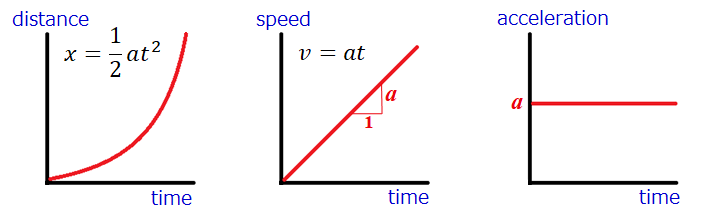
Consider, for instance, the relationship between vehicle speed and time as shown in the central graph. Here, the car’s speed increases linearly over time. Since the graph’s slope is constant, the acceleration in this scenario is also constant, as shown in the right-hand graph.
Vehicle speed also has a direction. However, like earlier, we’ll only consider the vehicle’s speed in its travel direction. Essentially, vehicle speed is how quickly the distance traveled changes over time.
To enhance our understanding, let’s add a graph to the left of the previous figure, depicting the distance traveled over time. If the vehicle’s speed graph shows a linear increase over time, then the graph of distance traveled will display a quadratic increase.
How Does It Look in the Logged Data from a Race Car?
The following graph shows a car traveling at full throttle down the straight of a track, reaching maximum speed, braking, and passing the corner.
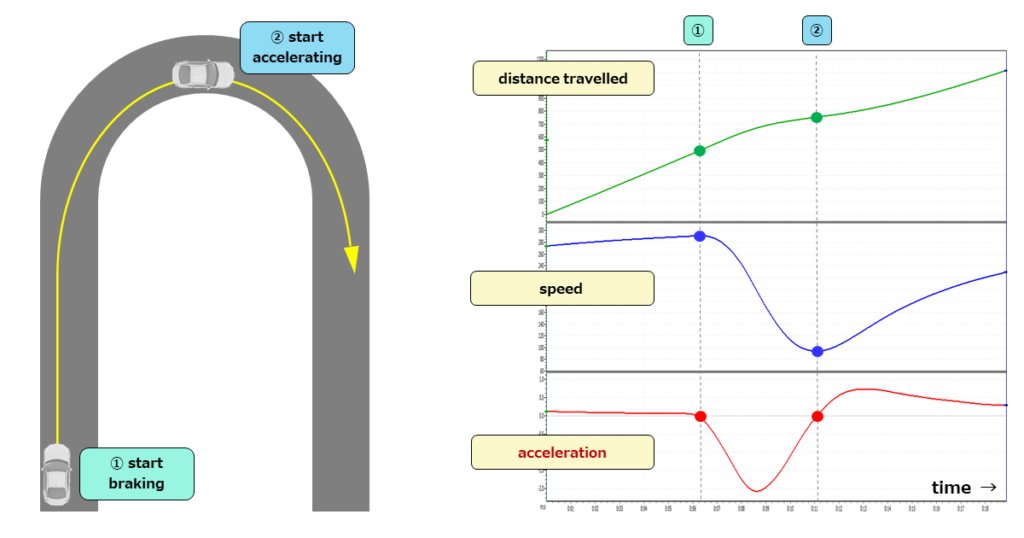
Earlier, we explained that acceleration is the rate of change in speed.
First, when the vehicle is running in a straight line before the corner, the speed graph shows a slight rightward movement, i.e., the vehicle is accelerating slightly.
In other words, since the car is accelerating slightly, the acceleration value at that time is slightly positive. The higher the vehicle speed, the greater the aerodynamic drag and, thus, the lower the acceleration.
At point 1, where the car reaches its maximum speed, the acceleration value changes from positive to negative and then momentarily drops to zero.
As braking begins, the slope of the speed becomes negative, and at the point where the slope is greatest, the acceleration is at a minimum.
At point 2, where the speed drops the most, the acceleration changes from negative to positive and then momentarily reaches zero.
From there, acceleration begins, but it eventually peaks, and from there on, as the speed increases, the acceleration gradually decreases.
We also explained that speed is the rate of change in distance traveled.
Unlike acceleration, speed is not negative unless the vehicle is running backward, so the slope of the distance traveled is never negative and always increases steadily.
However, it can be seen from the graph that the slope of the distance traveled is large when the speed is high and small when the speed is low.
Revisiting Newton’s Second Law of Motion
Now that we understand the concept of acceleration let’s return to Newton’s second law of motion.
We have seen that when a force is applied to an object, the object accelerates in the same direction as the force.
If no force is acting on the vehicle, the acceleration is zero.
Zero acceleration means no change in velocity. In other words, it is running at a constant speed or standing still. When the vehicle is in any other motion, it is under some external force. The force can be the driving force generated by the engine, the braking force by the brakes, air resistance, and so forth.
Acceleration During Cornering
Earlier, I explained that without an external force, acceleration is zero. That is, the vehicle is either stationary or running at a constant speed. This is the case when only acceleration in the direction of travel is considered.
Even if the vehicle is running at a constant speed, an external force is required for the vehicle to corner. Specifically, it is the grip of the tires. If the tires do not grip, the car cannot corner.
This will be explained in detail in another post.
Conclusion
In the fast-paced world of race cars, the combination of acceleration and Newton’s second law of motion reveals a complex interplay of forces and dynamics. Whether on straight paths or navigating tight corners, engineers and drivers need to comprehend these principles. Understanding the role of acceleration in determining a race car’s path adds a new layer of excitement to the racing experience, connecting the thrill on the track to the basic principles of motion and force.




