In the world of racing, the term “lateral G-force” is often heard. “G” stands for gravity and is originally a unit of acceleration. An acceleration of 1G is equivalent to the acceleration due to free fall. However, “lateral G” typically refers to the sideways force experienced by drivers during cornering. To clarify, we use the term “lateral G-force”. This article aims to explore how lateral G-force is generated and how it relates to acceleration.
Table of Contents
Speed and Longitudinal Acceleration
A car can move in various directions, but when it moves in the direction it’s facing, its speed refers to its forward and backward motion. The rate at which this speed changes over time is the car’s acceleration. For more details, please refer to the linked article.
Acceleration and Newton’s Second Law of Motion: The Key Role in Race Car Dynamics
Considering the Direction of Velocity
Even if a car is traveling at a constant speed, turning the steering wheel changes the direction of travel. When driving along a curve, the direction constantly changes. The original definition of velocity is the rate of change in position over time. Position is a vector quantity, represented by direction and distance from a reference point.
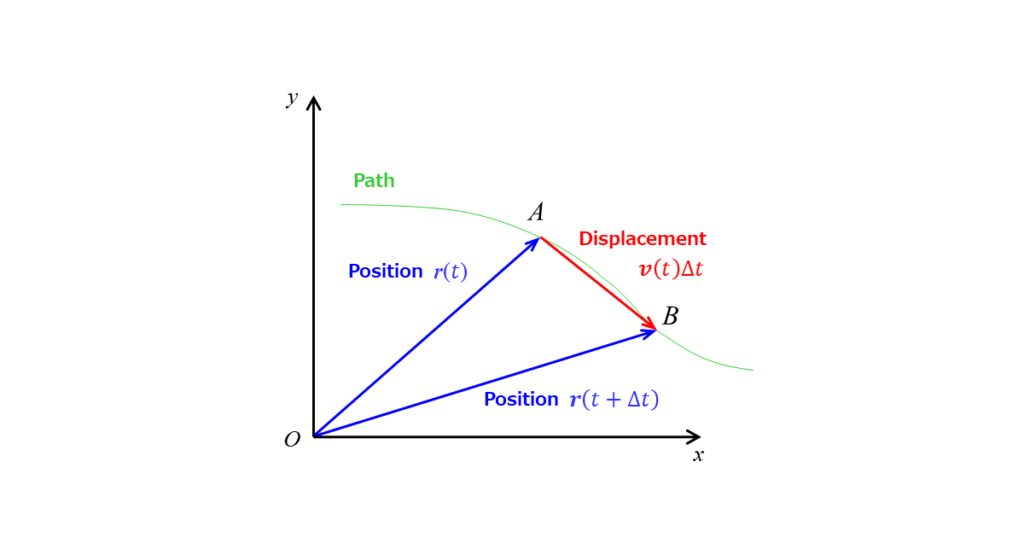
In the diagram below, at time t, an object is at point A, represented by the position vector r(t), and moves to point B over time Δt. The change in position, or displacement, is shown by the red arrow. As Δt approaches zero, the displacement vector aligns with the direction along the path at point A, indicating the direction of velocity.
Velocity is similar to speed but differs in that it is a vector quantity, meaning it includes both magnitude and direction, while speed only measures magnitude without direction.
Considering the Direction of Acceleration
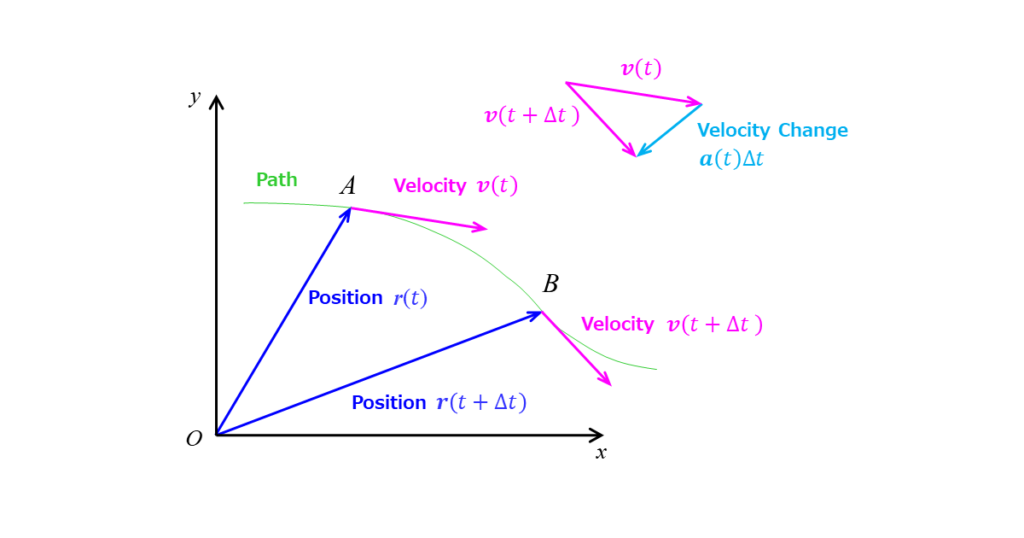
In the diagram below, the object moves from position A to B over time Δt. The velocities at positions A and B are in the direction along the path.
By aligning the start points of the velocity vectors, we can visualize the change in velocity, represented by the light blue arrow. Even if the magnitudes of the two velocity vectors are the same, a change in direction results in a change in velocity, and consequently, acceleration occurs.
Acceleration in Uniform Circular Motion
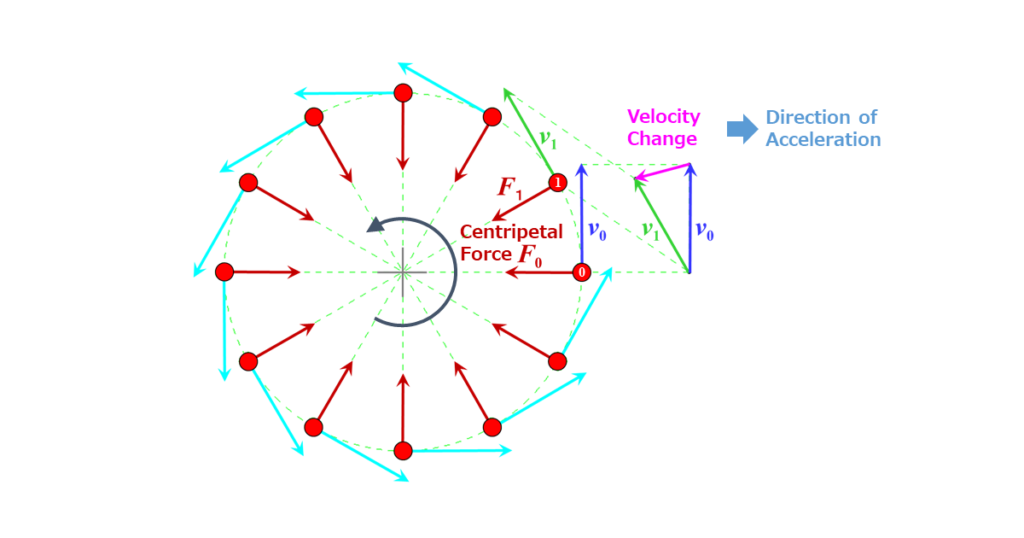
The direction of acceleration is the same as the direction of velocity change. In the diagram below, consider an object at position zero with its velocity vector represented by the blue arrow. If the object moves to position one after time Δt, its new velocity vector is shown by the green arrow. By paralleling these two vectors, the change is represented by the pink arrow. As Δt becomes smaller, the pink arrow’s direction becomes horizontal, perpendicular to the original blue velocity vector. This direction is the direction of acceleration, pointing towards the center of the circle.
Centripetal Force and Newton’s Second Law of Motion
The occurrence of acceleration implies, according to Newton’s Second Law of Motion, that a force is acting in the same direction. This force, directed towards the center of the circle, is known as the centripetal force. In vehicles, this force is primarily generated by the grip of the tires.
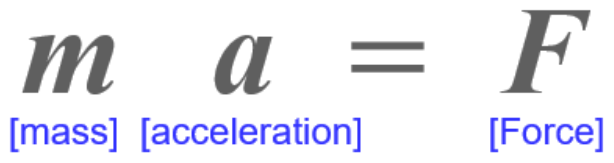
Centrifugal Force and d’Alembert’s Principle
To the occupants inside the vehicle, it feels as though they are being pulled outward, opposite to the tire’s grip, especially during cornering. This sensation is known as centrifugal force, often referred to as lateral G-force in racing contexts. This force can be well explained using d’Alembert’s principle, which states that the external force, in this case, the centripetal force, is always balanced by an inertial force acting in the opposite direction of acceleration. This inertial force is the essence of centrifugal force.
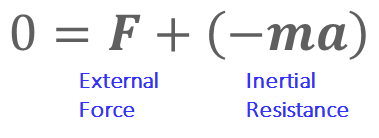
While the centripetal force acts at the tire-ground contact point, the inertial force acts on the entire vehicle, including the occupants, making them feel the centrifugal force. For more details on d’Alembert’s principle, please refer to the linked article.
Inertia Forces in Vehicle Dynamics: Are They Apparent Forces or Real Forces?
Conclusion
In this article, we delved into the concept of lateral G in racing cars. Lateral G is the sideways force felt by drivers during cornering, known as centrifugal force. Changes in the direction of velocity lead to acceleration, which in turn generates centripetal force, mainly due to tire grip.
Inside the car, occupants feel a force in the opposite direction of the tire’s grip. This is the centrifugal force, experienced as lateral G. Understanding this force as an inertial resistance to the vehicle’s acceleration, as explained by d’Alembert’s principle, helps clarify its nature. It’s important to note that the direction of acceleration and inertial force are opposite.



